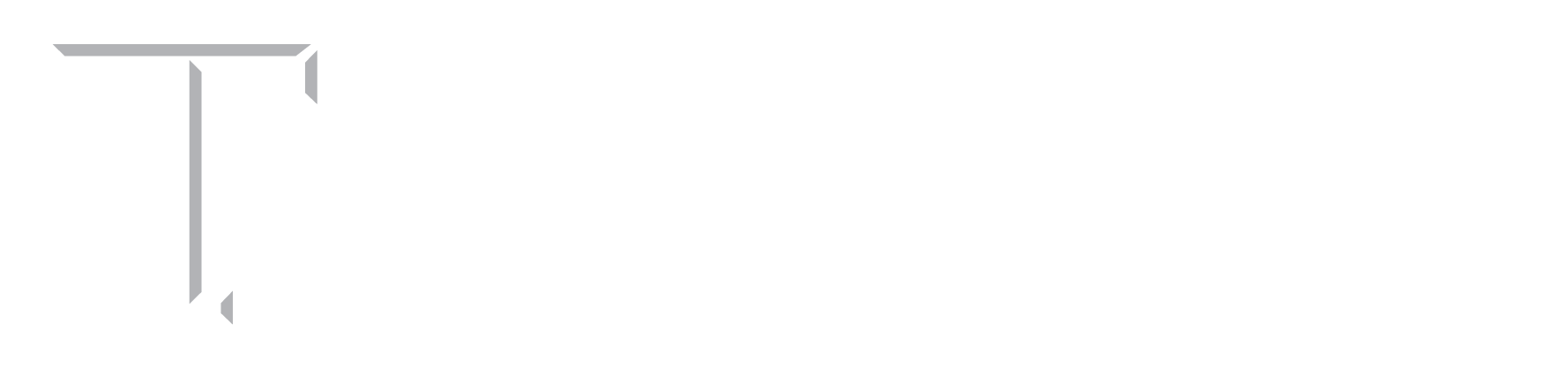da Vinci
The following sketches were found in Leonardo da Vinci’s notebooks. The concept was that by hanging a weight over a pulley, a known constant force could be applied horizontally to a block until sliding occurred. The static friction coefficient was then calculated by:
μs = mweight / mblock.
(Marder, 2004)
Inclined Plane
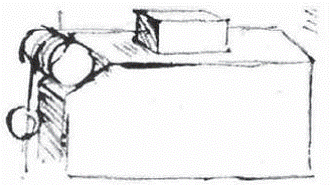
In this method, a block of mass, m, is placed on an inclined plane of angle, θ. By observing the angle at which the block begins to slide, the static coefficient of friction can be calculated with the use of this free body diagram and force balance.
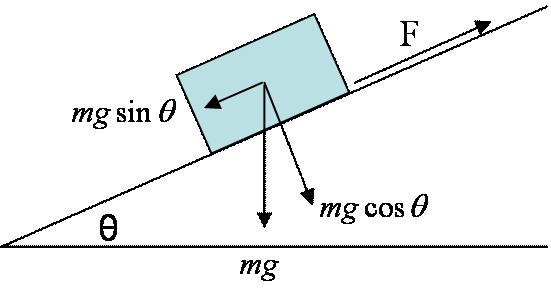
Again, the friction coefficient is defined as the ratio of the force parallel to the direction of motion to the force normal to the direction of motion, N. At the inception of sliding,
Spring Scale
This method involves pulling a mass, m, with a spring scale parallel to the surface. The static friction coefficient is calculated using the force required to start sliding while the kinetic friction coefficient uses the force required to maintain sliding. The forces are read from the spring scale and the coefficients are calculated.
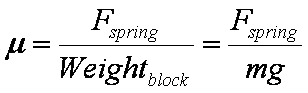
g: acceleration due to gravity = 9.81 m/s2
Clamping
In this method, only the static friction coefficient is calculated. An object is clamped between two surfaces using a known clamping force. The static friction coefficient is calculated using half of the force require to initiate movement because there are two mating surfaces.
Machine Controlled
The methods mentioned previously are mostly concerned with the static friction coefficient or the friction coefficient before wear occurs. With the use of machines, controlled testing can be conducted to investigate running-in, evolution of the friction coefficient, scuffing/seizure characteristics, and wear rates. These machines are discussed here.